Chapter 15 Confidence Intervals

Up to this point, we’ve focused on (1) the sample mean \(\bar{Y} = \frac{1}{N}\sum_{i=1}^N Y_i\) as an estimate of \(E(Y)=\mu\) and (2) the sample variance \(s^2 = \frac{1}{N-1}\sum_{i=1}^N \left( Y_i - \bar{Y}\right)^2\) as an estimate of \(V(Y)=\sigma^2\). Why is that? While the math is beyond the scope of this class, the main reason is because both are unbiased estimators of their respective population (or distribution) parameters.
An unbiased estimator is one where its expected value is equal to the population parameter, regardless of the sample size. Suppose we have a random sample \(\{Y_1, Y_2, \ldots, Y_N\}\), where \(Y\) has \(E(Y)=\mu\) and \(V(Y)=\sigma^2\). Because they are unbiased, \(E(\bar{Y}_N)=\mu\) and \(E(s^2)=\sigma^2\). For any particular sample, we don’t know exactly how close our estimate is to the population value. However, we can be reassured that the estimator (as a process) provides an accurate result on average.

Quite a few commonly used estimators are actually biased for small samples. Another desirable property, however, is consistency. The most intuitive notion of consistency is that as the sample size increases, (1) the bias decreases and (2) the variance of the estimator shrinks. Consider the following estimator of \(V(Y)\): \[s^{*2} = \frac{1}{N}\sum_{i=1}^N \left( Y_i - \bar{Y}\right)^2\] \(s^{*2}\) is a biased but consistent estimator of \(V(Y)=\sigma^2\). For any sample size \(N\), \(E(s^{*2})\ne \sigma^2\). However, for larger samples \(N\), the bias is relatively small. Moreover, as \(N\) increases, the bias shrinks and the variance of \(s^{*2}\) decreases.

Point Estimates versus Interval Estimates

Estimators like \(\bar{Y}_N\), \(s^2\), and \(s^{*2}\) provide us with a single value as an estimate. Because of that, we refer to such estimators as point estimates. As a single “best guess,” point estimates don’t provide us with any sense of uncertainty concerning the estimate. Is our estimate based on a lot of data or only a little? Do we think it is precise or that the population value might be far away?

In this chapter, we’ll explore interval estimates or confidence intervals. These are just what the name implies: estimates not just of a single value but of an interval of values. The width of the interval will (in part) reflect our uncertainty about the estimate.

Going forward, characterizing the uncertainty of an estimate will be just as important as calculating the estimate itself. In this chapter, we will take our first steps in statistical inference: learning about the population parameter based on our point estimate and the uncertainty associated with it. The combination of these two elements – the estimate and the uncertainty – not only provides a more complete picture of what we know about the population parameter, it also allows us to evaluate claims that are made about the population parameter.

15.1 Interval Estimates

As a concept, interval estimators can be difficult to understand at first. Let’s start with something we already know. Suppose we have a random sample of data \(\{ Y_1, Y_2, \ldots, Y_N\}\). We saw in the last chapter that the sample mean \(\bar{Y}_N\) will be a random variable with a distribution. It will have an expected value and a variance. Moreover, if the sample size is large enough, \(\bar{Y}_N\) will be approximately Normally distributed. Conceptually, that means that if we could repeatedly collect samples of size \(N\) and calculate the mean \(\bar{Y}_N\), those means would “bounce around” in terms of their values. Each sample will usually produce a slightly different mean.

Take a look at the interactive example below. Here, we’ll assume we’re drawing samples from a random variable \(Y \sim \mbox{Normal}(2, 100)\). The density shows the sampling distribution for \(\bar{Y}_{100}\). The blue line is \(E(Y)=\mu=2\). The black dot shows the value of \(\bar{Y}\) for a particular sample of \(N=100\) observations. Click on New Sample. This will generate a new sample of \(N=100\) observations and plot the sample mean (black dot). Repeat this a few times to reinforce the idea that different random samples will produce different values of \(\bar{Y}\).

Now check the box Show Interval. This will plot (as a gray bar) an interval around the mean. The red lines mark the lower and upper bounds of that interval. Click New Sample a few times. Each new sample produces a different sample mean, which in turn produces a different interval. As the mean bounces around, the interval bounces around with it. Just as the sample mean is a random variable, the gray interval is a random interval. That doesn’t mean that the size changes randomly — only that the lower and upper bounds change with the sample.

Ideally, we would like for our interval to be (1) narrow and (2) highly likely to contain the population \(E(Y)=\mu\) value. In the next section, we’ll examine the which factors that affect the width of our interval. For now, set the Interval Width slider to .1. This represents a very narrow interval estimate. Click New Sample a few times. Notice that the interval often doesn’t contain \(E(Y)=\mu=2\) — i.e., it doesn’t intersect with the blue line. That’s certainly not desirable. Now set Interval Width to .9, a wide interval. Click New Sample many times. The estimated interval will contain \(E(Y)=\mu=2\) almost every time.

Let’s formalize this a bit more. Suppose we use a process (or equation) for estimating the bounds of the interval \([L, U]\), where \(L\) and \(U\) correspond to the lower and upper values of the interval, similar to the red end-points of the gray bars in the previous example. Although it’s not the case for all confidence intervals, the ones we’ll focus on will be symmetric and centered around \(\bar{Y}\). In other words, we can express the lower and upper bounds as \[\begin{align*} L = \bar{Y} - \Delta\\ U = \bar{Y} + \Delta \end{align*}\] where \(\Delta\) determines the width of the interval.

With this, we can now define an important component of our interval estimate: the risk level \(\alpha\) and, correspondingly, the confidence level, which is expressed either as a probability \((1-\alpha)\) or as a \(100 \times (1-\alpha)\) percent. The confidence level \((1-\alpha)\) is defined as \[\begin{align*} (1-\alpha ) &= \Pr( L \le \mu \le U)\\ &= \Pr(\bar{Y}-\Delta \le \mu \le \bar{Y}+\Delta) \end{align*}\] In words, \((1-\alpha)\) is the probability that our interval estimates \(L\) and \(U\) contain \(E(Y)=\mu\). It’s important to note that \(\mu\) is not a random variable. \(E(Y)=\mu\) is a fixed population value. Rather, \(L\) and \(U\), the interval bounds, are the random variables. That’s easier to see in the second line above, where the bounds are expressed in terms of \(\bar{Y}\).

In the following sections, we’ll examine how \(\Delta\) is defined when estimating intervals for (1) the population mean \(\mu\) or (2) the population proportion \(\pi\).

15.2 Large-Sample Confidence Intervals for the Population Mean

Suppose we have a sample \(\{Y_1, Y_2, \ldots, Y_N\}\) drawn from random variable \(Y\), where \(E(Y)=\mu\) and \(V(Y)=\sigma^2\). Further, suppose our sample size \(N\) is large enough for the Central Limit Theorem to be a good approximation. The Central Limit Theorem tells us that \(\bar{Y}_N \sim \mbox{N}\left(\mu, \frac{\sigma^2}{N}\right)\). We can use this information to determine the value of \(\Delta\) for a \((1-\alpha)\) confidence interval for the population mean \(E(Y)=\mu\).

Recall that any Normally distributed random variable can be expressed as a Z-score. In the following, we’ll (1) define the \((1-\alpha)\) CI in terms of a \(Z\) random variable, (2) express the Z-score in terms of \(\bar{Y}\), and (3) rearrange terms until the value of \(\Delta\) is apparent: \[\begin{align*} (1-\alpha) &= \Pr(-Z_{\alpha/2} \le Z \le Z_{\alpha/2})\\ &= \Pr\left(-Z_{\alpha/2} \le \frac{\bar{Y_N}-\mu}{\sigma_{\bar{Y}_N}} \le Z_{\alpha/2}\right)\\ &= \Pr\left(-Z_{\alpha/2} \, \sigma_{\bar{Y}_N} \le \bar{Y_N}-\mu \le Z_{\alpha/2} \, \sigma_{\bar{Y}_N} \right)\\ &= \Pr\left(\bar{Y_N}-Z_{\alpha/2} \, \sigma_{\bar{Y}_N} \le \mu \le \bar{Y_N}+ Z_{\alpha/2} \, \sigma_{\bar{Y}_N}\right) \\ &= \Pr\left(\bar{Y_N}-Z_{\alpha/2} \, \frac{\sigma}{\sqrt{N}} \le \mu \le \bar{Y_N}+ Z_{\alpha/2} \, \frac{\sigma}{\sqrt{N}}\right) \end{align*}\]

The last line above implies that our large-sample confidence interval is the interval \[\left[ \bar{Y_N}-Z_{\alpha/2} \, \frac{\sigma}{\sqrt{N}}, \, \bar{Y_N}+Z_{\alpha/2} \, \frac{\sigma}{\sqrt{N}} \right] = \bar{Y_N}\pm Z_{\alpha/2} \, \frac{\sigma}{\sqrt{N}}\] Let’s take a second to dissect this. First, notice that the interval is centered around the sample mean \(\bar{Y}_N\). Second, the interval half-width, or margin of error, is \(\Delta = Z_{\alpha/2} \, \frac{\sigma}{\sqrt{N}}\). The interval width is a function of

  • \(\sigma\), the standard deviation of \(Y\) 
  • \(N\), the sample size
  • \(Z_{\alpha/2}\), the Z value associated with \(\alpha\) probability split between the two tails of the Standardized Normal distribution  

The margin of error (and interval width) will be larger when

  • \(Y\) has a larger variance \(V(Y)=\sigma^2\)
  • The sample size \(N\) is smaller
  • We choose a smaller risk \(\alpha\), requiring a larger value of \(Z_{\alpha/2}\)

Technically, the above version of the \((1-\alpha)\) CI requires that we also know \(\sigma\). In practice, we almost never do. However, when the sample size is large enough, \(\sigma^2\) is estimated by the sample variance \(s^2 = \frac{1}{N-1} \sum_{i=1}^N \left( Y_i - \bar{Y}_N \right)^2\) with enough precision. Substituting the sample standard deviation \(s\) for \(\sigma\), our \((1-\alpha)\) CI for the population mean is \[\begin{equation} \left[ \bar{Y}-Z_{\alpha/2} \, \frac{s}{\sqrt{N}}, \,\,\, \bar{Y}+Z_{\alpha/2} \, \frac{s}{\sqrt{N}} \right] \tag{15.1} \end{equation}\] where I have dropped the \(N\) subscript on the sample mean for easier reading.

Example 1

Suppose we have a random sample of data on morning commute times to work. We have \(N=100\) observations. We calculate the sample mean \(\bar{Y} = 45.8\) minutes and the sample variance \(s^2 = 243.2\). What is the 95% CI for the population mean?

95% confidence level \(\longrightarrow\) \(\alpha=.05\)

\(Z_{.05/2} = Z_{.025} = -1.96\). We can find this in R using qnorm():

> alpha = .05
> qnorm(alpha/2)
[1] -1.96

The standard error of \(\bar{Y}_N\) is \[\begin{align*} se(\bar{Y}_N) &= \frac{s}{\sqrt{N}}\\ &= \sqrt{\frac{243.2}{100}}\\ &= 1.559 \end{align*}\]

The 95% CI is therefore \[\left[ \bar{Y}-Z_{\alpha/2} \,\, se(\bar{Y}), \,\,\, \bar{Y}+Z_{\alpha/2} \,\, se(\bar{Y}) \right]\] \[\left[ 45.8-1.96 \, (1.559), \,\, 45.8+1.96 \, (1.559)\right]\] \[\left[ 42.74, \, 48.86 \right]\]

Example 2

Let’s take the same setup as in Example 1, except now we have a sample of \(N=300\) observations. (Note: Usually, the larger sample will have a slighly different mean than the smaller sample, but we’ll assume it’s the same for this exercise.) What is the 95% CI for the mean?

We already have the following:

  • \(N=300\)
  • \(\bar{Y}=45.8\)
  • \(s^2 = 243.2\) \(\longrightarrow\) \(s = \sqrt{243.2} = 15.59\)

The standard error in this case is \(se(\bar{Y}) = \frac{s}{\sqrt{N}} = \frac{15.59}{\sqrt{300}} = .9001\)

Notice that, compared to Example 1, the standard error has decreased, given the larger sample size. The 95% CI is now \[\left[ 45.8-1.96 \, (.9001), \,\, 45.8+1.96 \, (.9001)\right]\] \[\left[ 44.04, \, 47.56 \right]\] With a larger sample size, \(N=300\), the 95% CI is narrower (i.e., more precise) than when we used a sample of \(N=100\).

Example 3

Let’s return to Example 1 again and a sample size of \(N=100\). However, suppose we want to reduce our risk \(\alpha\) — i.e., we want a higher confidence level \((1-\alpha)\). What is the 99% CI for the mean?

Again, we know the following:

  • \(N=100\)
  • \(\bar{Y}=45.8\)
  • \(s^2 = 243.2\) \(\longrightarrow\) \(s = \sqrt{243.2} = 15.59\)

Now, a 99% CI means that \(\alpha=.01\). We need to find the Z value associated with \(\alpha/2\) probability in each tail of the Standardized Normal distribution:

> alpha = .01
> qnorm(alpha/2)
[1] -2.576

Notice that compared to Example 1 (with \(\alpha=.05\)), the Z value for \(\alpha=.01\) is larger. The 99% CI is \[\left[ 45.8-2.576 \, (1.559), \,\, 45.8+2.576 \, (1.559)\right]\] \[\left[ 41.78, \, 49.82 \right]\] With a lower risk \(\alpha=.01\) (or higher confidence level), the 99% CI is wider than when we constructed a 95% CI.

15.3 Large Sample Confidence Intervals for the Population Proportion

At this point, we’re going to start differentiating the sample mean and the sample proportion. For the sample mean \(\bar{Y}\), we’ll continue to assume that the underlying random variable \(Y\) can take many values — e.g., that it’s distributed Uniform, Normal, Exponential, Poisson, etc. We’ll assume that there is a true population (or distribution) expected value \(E(Y)=\mu\) and population variance \(V(Y)=\sigma^2\).

For the sample proportion, we’ll assume the underlying random variable \(Y \in \{0, 1\}\) is distributed \(\mbox{Bernoulli}(\pi)\). As we’ve previously seen, \(E(Y)=\pi\) and \(V(Y)=\pi (1-\pi)\). We’ll estimate the sample proportion just as we’ve done before, but now we’ll denote the estimate (and estimator) as \(p\): \[p_N = \frac{1}{N} \sum_{i=1}^N Y_i\]

The construction of a \((1-\alpha)\) confidence interval for the population proportion \(E(Y)=\pi\) is conceptually the same as that for the population mean. Assuming the population \(E(Y)=\pi\) isn’t too close to 0 or 1, we’ll appeal to the Central Limit Theorem and a sufficiently large sample size \(N\). Based on the CLT, the sample proportion \(p\) will be approximately Normally distributed with expected value \(E(p) = E(Y) = \pi\) and variance \(V(p) = \frac{V(Y)}{N} = \frac{\pi (1-\pi)}{N}\).

To construct the confidence interval, we’ll again use \[\begin{equation} \left[ p-Z_{\alpha/2} \,\, se(p), \,\,\, p+Z_{\alpha/2} \,\, se(p) \right] \end{equation}\] However, rather than using the sample variance \(s^2\) in our estimate of the standard error, we’ll use \[\begin{align*} se(p) = \sqrt{\frac{p\, (1-p)}{N}} \end{align*}\] Therefore, a large-sample \((1-\alpha)\) CI for the population proportion is \[\begin{equation} \left[ p-Z_{\alpha/2} \,\, \sqrt{\frac{p\, (1-p)}{N}}, \,\,\, p+Z_{\alpha/2} \,\, \sqrt{\frac{p\, (1-p)}{N}} \right] \tag{15.2} \end{equation}\]

Example 4

Suppose we have randomly sampled \(N=150\) US residents, asking each whether they are in favor of a Covid-19 mandate for the workplace (\(Y=1\)) or not in favor of a mandate (\(Y=0\)). The sample proportion of those in favor of a vaccine mandate is \(p=.58\). What is the 95% CI for the population proportion?

We know that

  • \(p=.58\)
  • \(N=150\)
  • 95% CI \(\longrightarrow\) \(\alpha=.05\) \(\longrightarrow\) \(Z_{\alpha/2}=Z_{.025}=1.96\)

Therefore, the 95% CI for the population proportion is \[\left[ .58-1.96 \, \sqrt{\frac{.58 (.42)}{150}}, \,\,\, .58+1.96 \, \sqrt{\frac{.58 (.42)}{150}} \right]\] \[\left[ .501,\,\, .659 \right]\]

As with confidence intervals for the population mean, the sample size \(N\) and the risk level \(\alpha\) affect the width of the interval. If we collect more data — i.e., increase \(N\) — the standard error will be smaller. If we choose a lower risk (or higher confidence), the associated Z value will be larger in magnitude, so our interval will be wider.

15.4 Interpreting Confidence Intervals

We saw in Example 4 that the 95% CI for the population proportion was \(\left[ .501,\,\, .659 \right]\). How do we interpret this? There is a (quite common) incorrect interpretation and a (slightly tedious) correct interpretation.

Incorrect Interpretation: There is .95 probability that the population proportion \(\pi\) is between .501 and .659.

The problem with the above interpretation is that it is a misreading of the fundamental definition of the confidence interval: \[\Pr( L \le \pi \le U) = (1-\alpha)\] The issue is that the incorrect interpretation poses the population parameter \(\pi\) as the random variable. However, as we noted before, \(\pi\) (or \(\mu\) for the mean) is a fixed population parameter. The interval end points \(L\) and \(U\) are the random variables. We can estimate \(L\) and \(U\) as we have done above — .501 and .659, respectively. The common inclination is then to mentally substitute the estimates of \(L\) and \(U\) into the above equation, which makes it look like \(\pi\) is now the random variable. But it’s not. \(E(Y)=\pi\) is the unknown, fixed population parameter.

Can we at least say whether \(\pi\) is in the interval \([.501, .659]\)? Unfortunately, no. The definition of a CI is a statement that, in repeated random sampling, our random interval \([L, U]\) will contain the population parameter \(\pi\) with probability \((1-\alpha)\), or \(100\times (1-\alpha)\)% of the time. However, we don’t know the true value of \(\pi\) — that’s why we’re doing this in the first place. Once we’ve drawn a particular sample, calculated the sample proportion, and constructed the confidence interval, we simply have no idea whether it contains \(\pi\) or not.

So, what can we say? The full, technically correct interpretation is rather verbose, especially if we have to repeat it each time we interpret a confidence interval.

Correct Interpretation: In repeated random sampling, calculating a 95% confidence in this way (Equation (15.2)) will produce confidence intervals that contain the population parameter 95% of the time. For this specific sample, the sample proportion is \(p=.58\) and the 95% CI is \([.501, .659]\).

In practice, we state the last line and leave the preamble as understood. And that’s it! Again, we don’t know if the true proportion \(E(Y)=\pi\) is contained within that interval or not. We are trusting the process — the math behind the equation — to provide us with accurate interval estimates, given a chosen level of risk \(\alpha\). As we’ll see in the next interactive example, that’s not a blind leap of faith, especially if we have a relatively large sample size \(N\).

Finally, although we have discussed interpretation in terms of the population proportion \(\pi\), it should be clear that we interpret a \((1-\alpha)\) confidence interval for the population mean \(\mu\) in exactly the same way.

Interactive Example: Confidence Intervals

In this example, we’ll examine how confidence intervals change as we change the sample size \(N\) and the confidence level \((1-\alpha)\).

In the default configuration of the app below, 100 samples have been generated from a Normal distribution. Each sample consists of \(N=100\) observations. For each sample, the mean is calculated and a 95% confidence interval is constructed (i.e., \(\alpha=.05\)). The graph in the main panel displays each of the 95% confidence intervals as a horizontal gray bar. The lower bound for a CI is the leftmost value of the gray bar. The upper bound is the rightmost value. The sample mean is shown as a black dot.

The first thing thing to notice is simply the variability in the confidence intervals. Each random sample consists of a slightly different set of values, resulting in a different sample mean and, ultimately in different bounds for the CI.

In the real world, where we only collect a single sample of data, we hope that our CI contains the true expected value \(E(Y)\) for our distribution or population. \(E(Y)\) is shown as a blue line in the graph. At the bottom of the left panel, there’s a box labeled “Order the CIs.” Click that box. This will order the confidence intervals by their means. Now it’s a little easier to see which CIs contain \(E(Y)\) — they will be located at the very top and very bottom of the graph. The 95% CIs that do not contain \(E(Y)\) are the gray bars that do not overlap with the blue line for \(E(Y)\). Approximately, 5% of the CIs will not contain \(E(Y)\). The percentage of CIs that do not contain \(E(Y)\) is shown just below the graph.

With only 100 samples (and CIs) generated, the number below the graph may be quite different from 5%. As you increase the number of samples generated (left panel) to 10,000, the percentage of CIs that don’t contain \(E(Y)\) will tend to be closer to the \(100 \times (1-\alpha)\)% confidence level. Try that now. Note that it will take longer for the app to refresh and it will be more difficult to see the individual confidence intervals. Make sure you have the CIs ordered to view them more easily. At this point, move the slider for \(\alpha\) to different values. When you increase \(\alpha\) to .1, you should see below the graph that roughly 10% of the CIs did not contain \(E(Y)\). Increase \(\alpha\) to .2 and roughly 20% of the CIs will not contain \(E(Y)\).

At this point, set \(N=100\), \(\alpha=.05\), and the number of samples generated to 100. Make sure the CIs are ordered. Let’s take a look at how the width of a CI changes as we change the sample size \(N\). First, note the width of the CIs in the graph. Now change the sample size to \(N=200\). What happened? Change the sample size to \(N=300\), then 500, then 1000. As the sample size increases, the standard error \(se(\bar{Y}) = \sigma^2/\sqrt{N}\) decreases, and the width of the CI therefore decreases.

Now, let’s look at how the CI changes as we change the \((1-\alpha)\) confidence level. Set \(\alpha=.01\). That corresponds to a 99% confidence level. Note the width of the CIs. Now increase \(\alpha\) to .05, corresponding to a 95% confidence level. How did the width of the CIs change? As before, increase \(\alpha\) to .1 and then to .2. As we increase our risk \(\alpha\) from .01 to .05 to .1 to .2, we decrease the confidence level from 99% to 95% to 90% to 80%, respectively. Higher risk (lower confidence) produces narrower CIs. Lower risk (higher confidence) produces wider CIs.

Take some time to work through this interactive example. You can also select the Bernoulli distribution in the left panel. There, the sample mean \(\bar{Y}_N\) represents the sample proportion of 1’s.

15.5 Practical Uses of Confidence Intervals

Constructing a confidence interval requires that we estimate (1) the sample mean (or proportion) and (2) the standard error. The first is an unbiased estimator of the population mean. The second, the standard error, is an estimate of our uncertainty concerning the sample mean — e.g., how far the sample mean will bounce around in repeated random sampling. The mean by itself is useful, but not as useful as when we understand our uncertainty about it as well.

As an example, suppose a survey company reports that 52% of US residents favor tax incentives for electronic vehicle (EV) purchases. That implies \(p=.52\). Based on that estimate alone, it seems that a majority of US residents favor the EV tax incentives. Now suppose you dig a little deeper, find the number of people surveyed, calculate the standard error for \(p\), and you create a confidence interval. We’ll consider two different scenarios.

In the first scenario, you find that \(N=5000\) and you calculate a 99% CI of \([.502, .538]\). In this case, not only is the confidence level quite high (99%), but the interval is narrow. That’s what we hope for (but don’t always get!). We would conclude that our estimate of \(p=.52\) is a rather precise estimate.

In the second scenario, you find that \(N=50\) and you calculate a 95% CI of \([.38, .66]\). The sample proportion is the same as before, \(p=.52\). In this case, the standard error is quite large, resulting in a wide confidence interval. Our estimate of the population proportion does not appear to be very precise. We would be much more uncertain about the population proportion in this scenario.

These two examples demonstrate how our uncertainty, characterized by the standard error, can affect what we think we know about an estimate of the mean or proportion. Both cases have the same sample proportion. In the first scenario, that seems like an accurate estimate. In the second scenario, we’re not so sure how accurate it really is.

We can also use confidence intervals to evaluate claims about the sample mean or proportion. Let’s stay with the EV incentives example. Suppose a senator in your state claims that “The American people support EV tax incentives.” That’s a claim that \(\pi>.5\).

How would we evaluate that claim in the two scenarios above? In the first scenario, the 99% CI is \([.502, .538]\). In this case, \(p\) seems to be precisely estimated. Moreover, using a 99% confidence level, the lower bound is still greater than .5. It’s a little close (.502). However, it’s entirely plausible in this scenario that a majority of US residents support EV incentives.

Now consider the second scenario. Here, the 95% CI is \([.38, .66]\). Again, suppose a senator claims that over half of US residents support EV incentives. How would we evaluate this claim? Based on this CI, we have too much uncertainty. A large portion of the interval, [.38, .499], contradicts the senator’s claim. In this case, we wouldn’t conclude that the senator is definitely wrong. Instead, we would conclude that there simply isn’t enough evidence to support the senator’s claim.

The following are two more examples of how we can use confidence intervals to evaluate claims.

Example 5

You’re having Thanksgiving dinner with your family. Your loud uncle claims that there’s no reason to get the Covid-19 vaccine — that just as many vaccinated people are being hospitalized as unvaccinated people. You find here that from April 4 to June 19, 2021, there were 28,883 hospitalizations of people who were not fully vaccinated and 2,025 hospitalizations of people who were fully vaccinated. At face value, your uncle’s claim is clearly incorrect. However, let’s frame this as a proportion and create a confidence interval.

Let \(Y=1\) if a hospitalization is of a fully vaccinated person and \(Y=0\) if a hospitalization is of a person who is not fully vaccinated. The proportion of those hospitalized who were fully vaccinated is \(p=\frac{2,025}{2,025+28,883}=.0655\). \(N=2,025+28,883=30,908\).

The 99% CI for the population proportion \(\pi\) is \[\left[ .0655-2.576 \, \sqrt{\frac{.0655 (.9345)}{30,908}}, \,\,\, .0655+2.576 \, \sqrt{\frac{.0655 (.9345)}{30,908}} \right]\] \[[.0618, .0691]\]

If an equal number of those hospitalized were fully vaccinated, then the population proportion would be \(\pi=.5\). That is clearly far outside the 99% CI. We can safely conclude — at least for the period April 4 to June 19 — that your uncle’s claim is incorrect.

Example 6

You’re talking politics with three friends. Friend 1 claims that US senate races are usually not very close — that, due to various factors, the incumbent tends to win by quite a bit, say 60% of the two-party vote. Friend 2 claims the incumbent share is even larger on average: 70%. Your third friend claims elections in general are very very close, so the incumbent share should be 51% on average.

You find data on US senate races from 1980-2000. Each observation \(Y\) represents the percentage (0-100) of the two-party vote that an incumbent senator received in his or her state’s US senate election that year. There are \(N=296\) observations. The sample mean is \(\bar{Y}=61\)% and the sample standard deviation is \(s=9.932\). Based on that, you calculate the standard error to be \[se(\bar{Y}) = \frac{s}{\sqrt{N}} = \frac{9.932}{\sqrt{296}}=.5773\]

The 95% CI for the population mean \(\mu\) is \[\left[ 61-1.96 \, (.5773), \,\, 61+1.96 \, (.5773)\right]\] \[[59.86, \, 62.13]\] Let’s evaluate your friends’ claims now. Friend 3 claimed that elections are very close and that \(\mu=51\)%. Comparing that to the CI above, we see that it is well outside the 95% CI. It is not supported by the data. Friend 2 claimed that \(\mu=70\)%. That too is well outside the 95% CI. It is not supported by the data. Friend 1 claimed that \(\mu=60\)%. Comparing that to the 95% CI above, it is within the CI bounds. Although your friend’s claim differs slightly from the sample mean (61%), it is still plausible given the data and resulting confidence interval.

Practice Session: Large-Sample Confidence Intervals

In the practice session below, you are told (1) whether a random variable is continuous or binary, (2) the sample size \(N\), and (3) relevant information such as the sample mean or sample proportion. You are then asked to calculate a \(100\times (1-\alpha)\)% confidence interval for the population parameter.

Based on clues in the question setup, you will need to determine which type of confidence interval to use. Enter the lower and upper bounds of the interval in the corresponding boxes and click Submit. Click Next to try another problem. Complete five or six problems, or until you feel comfortable calculating different types of large-sample confidence intervals.

15.6 Margin of Error and Sample Size

It’s common when reading political news stories featuring election polls to see not just an estimate of the proportion of people who intend to vote for a candidate, but also a margin of error. As we’ve already seen, the margin of error is the half-width of a confidence interval. For a large-sample CI of the population proportion, the margin of error is \[\begin{equation} MoE = Z_{\alpha/2} \sqrt{\frac{p (1-p)}{N}} \tag{15.3} \end{equation}\] When we are analyzing data from an existing survey, we calculate the margin of error (and confidence interval) using the sample proportion \(p\) that we estimate from the data. We’ve already seen two examples (4 & 5 above) where we did this as part of constructing a confidence interval.

Suppose instead that we are designing a survey and we want to know how many people we should interview. The margin of error equation can also be used to determine the number of people \(N\) that need to be polled in order to achieve a particular margin of error. Referring to Equation (15.3), if we square both sides, we can then rearrange the terms so that we have the sample size \(N\) on the left-hand-side: \[\begin{align*} MoE^2 &= (Z_{\alpha/2})^2 \, \frac{p (1-p)}{N} \\ N & = (Z_{\alpha/2})^2 \, \frac{p (1-p)}{MoE^2} \end{align*}\] The sample size is now written as a function of the desired margin of error, the Z value associated with the risk level \(\alpha\), and the sample proportion \(p\). We can choose values for the margin of error and for the risk \(\alpha\). However, \(p\) is a value we’ll eventually estimate. Before we conduct the survey, we don’t know what it will be. If we want to be conservative, we can set \(p=.5\) for this calculation. That will produce the largest variance \(p(1-p)\). Any other value of \(0\le p \le 1\) will produce a smaller value of \(p (1-p)\).

With that, we now have the following equation for the sample size \(N\): \[\begin{equation} N = \left[ \frac{.5 \, Z_{\alpha/2}}{MoE} \right]^2 \tag{15.4} \end{equation}\] If we are designing a survey, we can choose a margin of error \(MoE\) and a risk \(\alpha\), and we can then calculate the sample size \(N\) that we’ll need in order to ensure that the post-survey margin of error is no larger than the value of \(MoE\) that we entered into Equation (15.4).

Finally, the norm for polls you’ll see in the news is to use \(\alpha=.05\) — i.e., a 95% confidence level. In that case, \[N = \left[ \frac{.5 \, (1.96)}{MoE} \right]^2\]

Example 7

A local politician hires you to conduct a poll to determine the proportion of eligible voters that intend to vote for her. She wants a 95% confidence level with a 3% margin of error. How many people will you need to interview?

We know that

  • 95% CI \(\longrightarrow\) \(\alpha=.05\) \(\longrightarrow\) \(Z_{\alpha/2}=1.96\)
  • \(MoE = .03\)

Plugging into Equation (15.4) \[\begin{align*} N &= \left[ \frac{.5 \, (1.96)}{.03} \right]^2\\ &= 1,067 \end{align*}\]

You should interview just over 1,000 people.

Example 8

Another politician contacts you to conduct a similar poll for him. However, he wants a 99% confidence level and a 1% margin of error. How many people will you need to interview?

We know that

  • 99% CI \(\longrightarrow\) \(\alpha=.01\) \(\longrightarrow\) \(Z_{\alpha/2}=2.576\)
  • \(MoE = .01\)

Plugging into Equation (15.4) \[\begin{align*} N &= \left[ \frac{.5 \, (2.576)}{.01} \right]^2\\ &= 16,589 \end{align*}\]

You’ll need to interview a lot more people in this case!

15.7 Small Sample Confidence Intervals for the Population Mean

The confidence intervals we’ve examined so far are all based on the assumption that we have a large enough sample that the Central Limit Theorem will provide a good enough approximation of the sampling distribution for our statistic. What do we do in the case where the sample size \(N\) is relatively small — say, \(N=24\)?

Student’s t Distribution

For small samples, we won’t use the Normal distribution and Z values. Doing so assumes that we have more certainty about our statistic than we actually have in small samples. Using the Normal in such cases produces confidence intervals that are too narrow. Instead, we’ll use Student’s t distribution, developed by William Gossett while he was working for the Guinness brewing company.

The t distribution is similar to the Standardized Normal in many ways. It is symmetric and has a similar “bell” shape. However, the t distribution takes an additional parameter: the degrees of freedom, \(df\). When the degrees of freedom are relatively small the t has noticeably “fatter” tails than the Normal. In other words the t distribution has more area under the density in its tails than does the Normal. As the degrees of freedom \(df\) increase, the t converges to the Standardized Normal. The two distributions are shown in the following graph. The Normal density is shown in black. The t density with \(df=3\) is shown in blue.

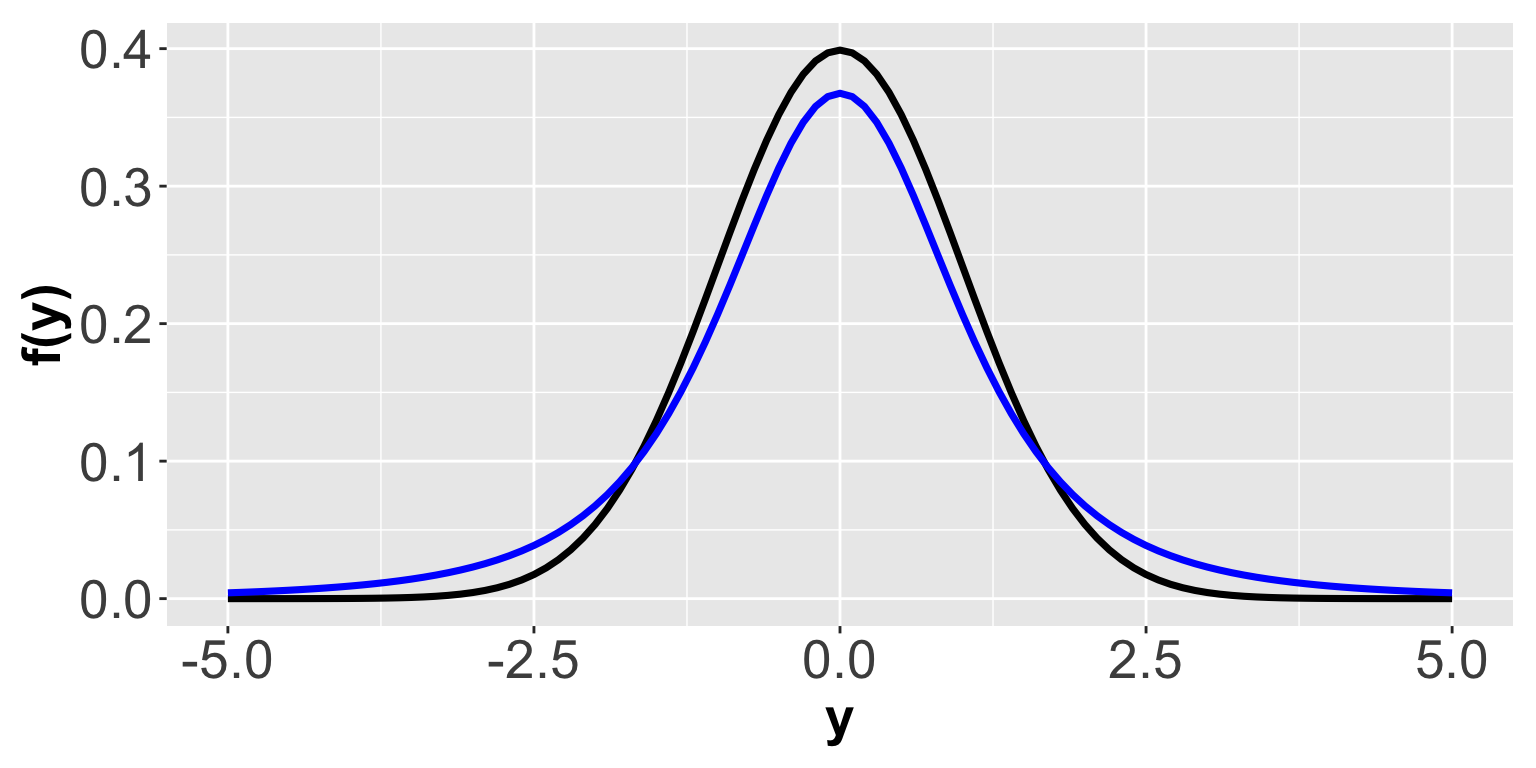
Gossett, publishing under the pseudonym “Student,” showed in a 1908 article that in small samples, a standardized version of the sample mean (similar to a Z-score) is not distributed Normal — it is distributed according to the t distribution.

Suppose we have a random variable \(Y\) with \(E(Y)=\mu\) and \(V(Y)=\sigma^2\), for small samples (e.g., \(N<50\)), the t statistic \[ t = \frac{\bar{Y}-\mu}{s/\sqrt{N}}\] will be distributed t with \(df=N-1\) degrees of freedom. Throughout this course, we will use R commands to calculate values related to the t distribution, so I do not provide the equation for its density \(f(y)\) here. However, if you’d like to read more on the t distribution, its Wikipedia page is a good place to start.

Small Sample Confidence Interval

The equation for a small-sample \((1-\alpha)\) CI for the population mean is similar to the large-sample version. The only difference is that we use a \(t_{df, \alpha/2}\) value, rather than a \(Z_{\alpha/2}\) value: \[\begin{equation} \left[ \bar{Y}-t_{N-1, \alpha/2} \, \frac{s}{\sqrt{N}}, \,\,\, \bar{Y}+t_{N-1, \alpha/2} \, \frac{s}{\sqrt{N}} \right] \tag{15.5} \end{equation}\]

How does using \(t_{N-1, \alpha/2}\) change the result compared to using \(Z_{\alpha/2}\)? The following graph shows, again, the densities for the Normal and the t with \(df=3\). Suppose we want to calculate a 95% CI in each case. That means we need to find the t and Z values associated with \(\alpha/2 = .025\) probability in each tail. In the plot below, the .025 tail probabilities are shown for each distribution: blue for the t and black for the Normal. The \(t_{df=3,.025}\) values are (\(\pm 3.182\)) and the \(Z_{.025}\) values are (\(\pm 1.96\)).

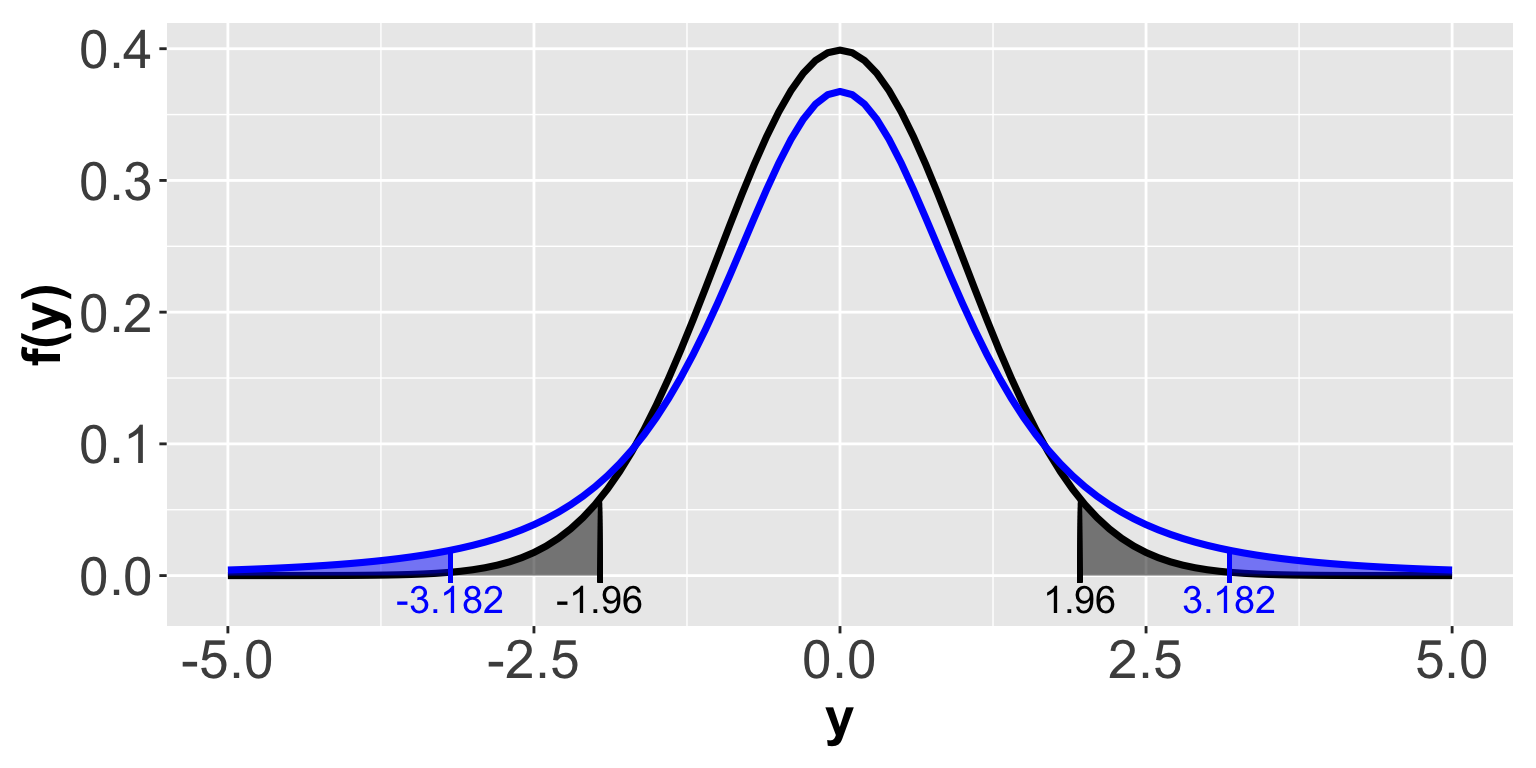Notice that the t values (\(\pm 3.182\)) are much larger in magnitude than the Z values (\(\pm 1.96\)). The larger t values will contribute to a wider CI. But that’s not all. The smaller sample size \(N\) will increase the standard error, which will in turn contribute to a wider CI. Therefore, all else equal, a 95% CI using the t will be wider than a 95% CI using the Normal, due in part to the larger t values and in part to the larger standard error. The wider interval reflects our uncertainty about the mean due to having such a small sample.

Example 9

Let’s repeat Example 1, but assume we have a much smaller sample.

Suppose we have a random sample of data on morning commute times to work. We have \(N=20\) observations. We calculate the sample mean \(\bar{Y} = 45.8\) minutes and the sample variance \(s^2 = 243.2\). What is the 95% CI for the population mean?

We have

  • \(\bar{Y}=45.8\)
  • \(N=20\) \(\longrightarrow\) \(df=N-1=19\)
  • \(s^2 = 243.2\) \(\longrightarrow\) \(se(\bar{Y}) = \sqrt{\frac{243.2}{20}} = 3.487\)

We need to find \(t_{df,\alpha/2} = t_{19, .025}\). We can use R and qt() to do so:

> qt(.05/2, df=19)
[1] -2.093

Now we plug everything into Equation (15.5). The 95% CI for the population mean is \[\left[ \bar{Y}-t_{N-1, \alpha/2} \, \frac{s}{\sqrt{N}}, \,\,\, \bar{Y}+t_{N-1, \alpha/2} \, \frac{s}{\sqrt{N}} \right]\] \[\left[ 45.8-2.093\, (3.487), \,\,\, 45.8+2.093 \, (3.487) \right]\] \[\left[ 38.5, \,\, 53.1 \right]\] This is obviously wider than the 95% CI in Example 1, \([42.74, \, 48.86]\), where the sample size was \(N=100\).

Example 10

Let’s repeat the same example, but now assume the sample size is \(N=75\).

We have

  • \(\bar{Y}=45.8\)
  • \(N=75\) \(\longrightarrow\) \(df=N-1=74\)
  • \(s^2 = 243.2\) \(\longrightarrow\) \(se(\bar{Y}) = \sqrt{\frac{243.2}{75}} = 1.8007\)

We can use qt() to find \(t_{74, .025}\):

> qt(.05/2, df=74)
[1] -1.993

Again, plugging everything into Equation (15.5), the 95% CI for the population mean is

\[\left[ 45.8-1.993\, (1.8007), \,\,\, 45.8+1.993 \, (1.8007) \right]\] \[\left[ 42.21, \,\, 49.39 \right]\] This is still slightly wider than the 95% CI in Example 1, \([42.74, \, 48.86]\), where the sample size was \(N=100\). However, we can see that as the sample size \(N\) increases, a \((1-\alpha)\) CI using the t will converge to a \((1-\alpha)\) CI using the Normal.

15.8 Summary

Practice Session: Confidence Intervals

This practice session is similar to the previous one for large-sample confidence intervals. In this case, you may be asked to calculate any of the following:

  • Large-sample CI for the population mean
  • Large-sample CI for the population proportion
  • Small-sample CI for the population mean
  • The sample size \(N\) needed to ensure a desired margin of error.

Enter your answer in the appropriate boxes and click Submit. Click Next to try another problem. Complete ten questions, or until you feel comfortable with the material.