Chapter 19 Joint Distributions, Independence, and Conditional Probability
Up to this point, we have examined the probability distributions of individual discrete random variables, such as the roll of a die or flipping a coin. Sometimes, however, two (or more) random variables may be related in some way, such that knowing the value of one RV provides information about the distribution of the other RV. The joint distribution of two random variables can be interesting in itself. Using the joint distribution, we can also calculate conditional probabilities.
Let’s consider the grim example of lung cancer. Current data suggests that a randomly selected US resident has a \(\frac{1}{16}\) chance of developing lung cancer in their lifetime. We can model this as a Bernoulli distribution, where the outcomes are \(Y \in \{ \mbox{No Lung Cancer}, \, \mbox{Lung Cancer} \}\) and \(\Pr(\mbox{Lung Cancer})=\frac{1}{16}\).
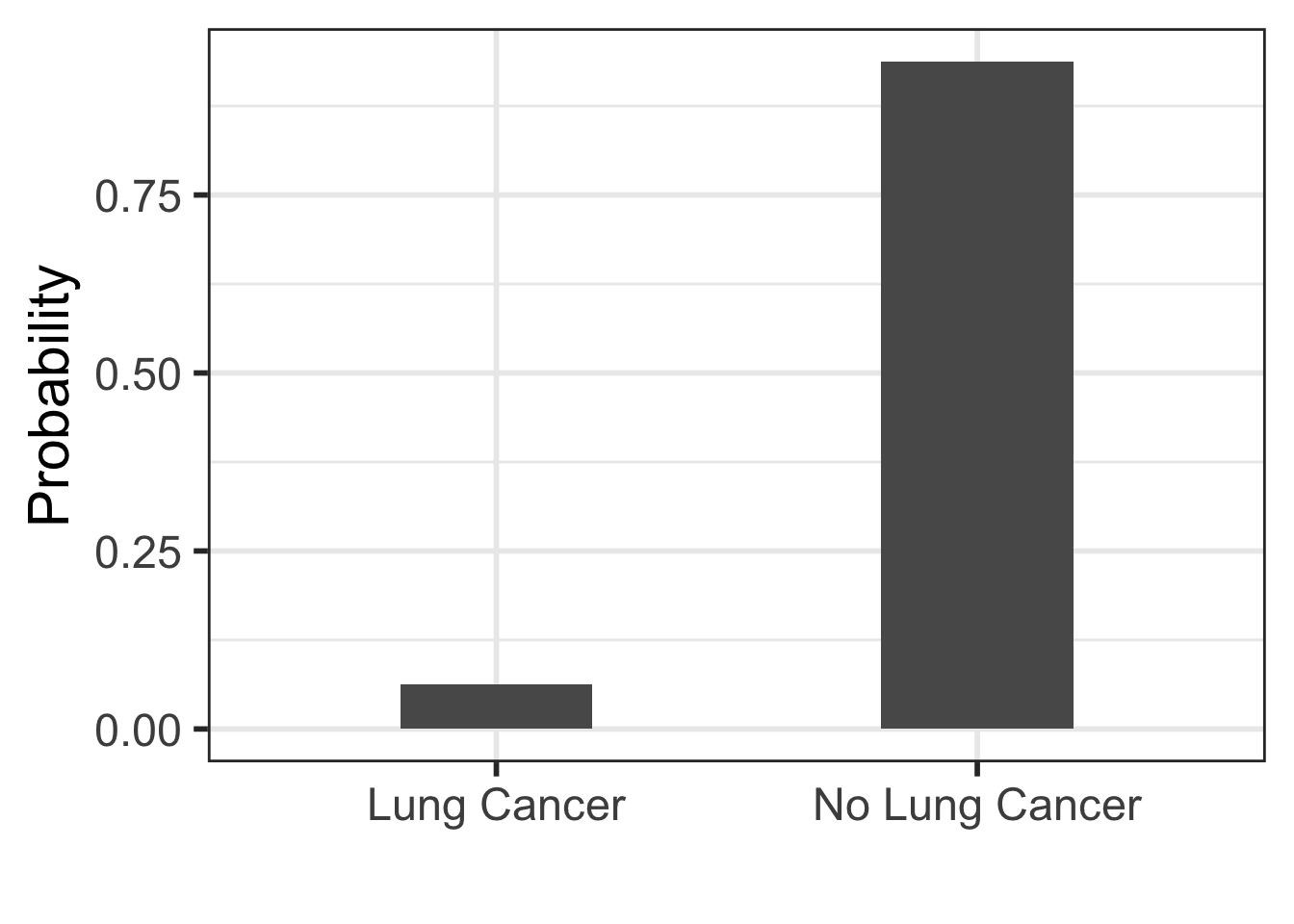
This example is similar to those we saw in previous chapters.
Now consider another random variable \(X\) that represents whether a person is a smoker or not: \(X \in \{ \mbox{Nonsmoker}, \, \mbox{Smoker} \}\). We might very well be interested in whether the probability of developing lung cancer differs depending on whether someone is a smoker or nonsmoker. Based on some additional information (here and here), we can compare the probability of developing lung cancer among smokers versus nonsmokers:
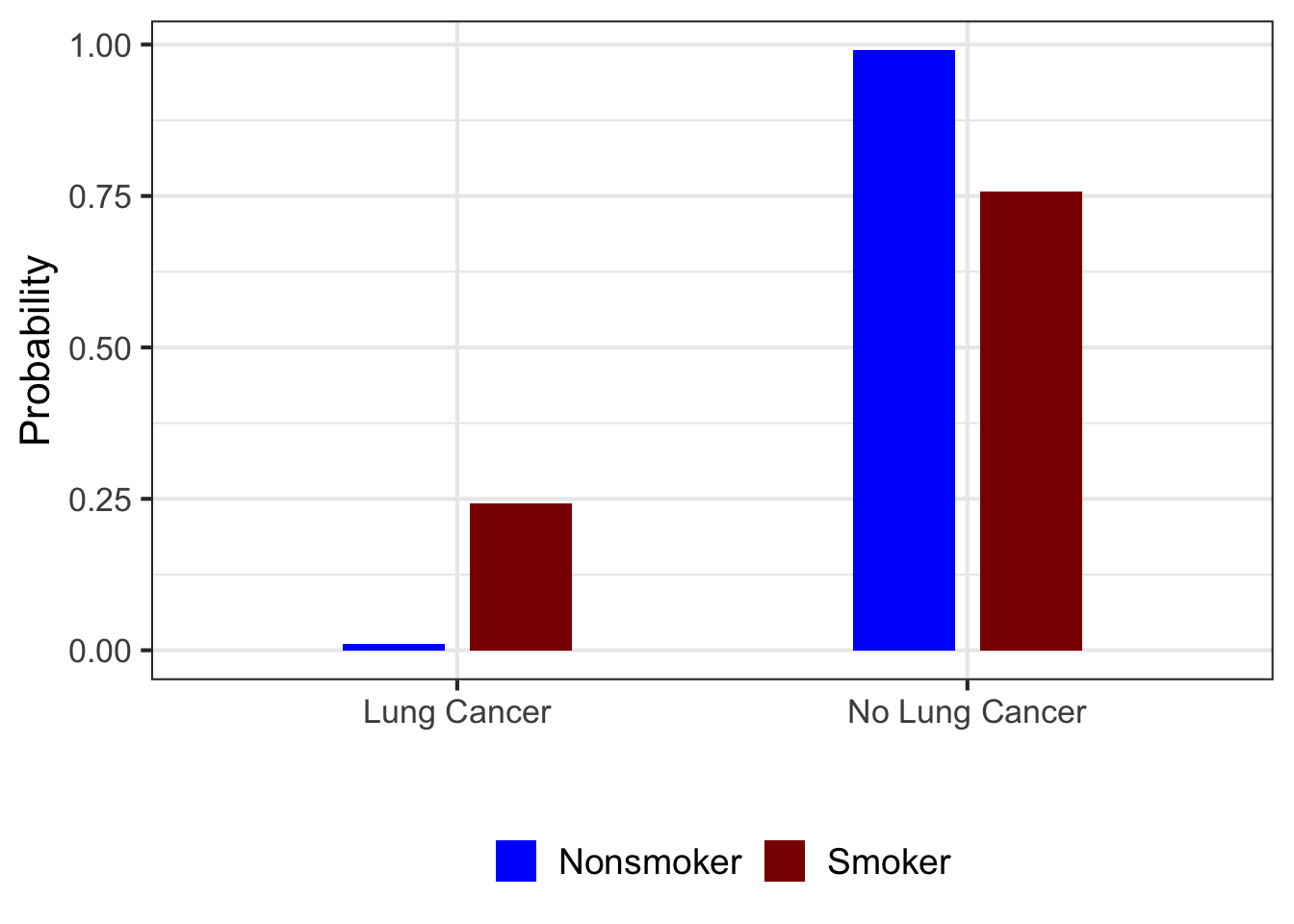
Not surprisingly, the probability distribution for developing lung cancer differs for smokers versus nonsmokers. Notice (on the left side of the graph) that the probability of lung cancer is 25 times higher for smokers than it is for nonsmokers.
In this chapter, we’ll look at relationships like the above, where we have two RVs that may be related in some way. We’ll want to characterize the joint distribution of the two RVs, assess whether the two RVs are independent, and then calculate conditional probabilities like those shown above.
19.1 Joint Probability Distribution for Two Discrete Random Variables
Let’s continue to use the previous example of lung cancer and smoking. However, we’ll slightly abbreviate the lung cancer labels: \[\begin{align} X & \in \{ \mbox{Nonsmoker}, \, \mbox{Smoker} \} \\ Y & \in \{ \mbox{No Cancer}, \, \mbox{Cancer} \} \end{align}\]
Now imagine that we have a database with every US resident in it, that we can randomly draw a person from this database, and that we then look at the values of \(X\) and \(Y\) for that person. How likely are we to draw (or observe) a person that is a nonsmoker who never gets cancer? How likely are we to draw someone that is a smoker who eventually gets cancer? These are the types of joint probabilities that are shown in the table below:
| Y | ||||
| No Cancer | Cancer | Pr(x) | ||
| X | Nonsmoker | 0.7657 | 0.0075 | 0.7732 |
| Smoker | 0.1718 | 0.055 | 0.2268 | |
| Pr(y) | 0.9375 | 0.0625 | ||
RV \(X\) and its possible outcomes { Nonsmoker, Smoker } are shown along the left side of the table. RV \(Y\) and its outcomes { No Cancer, Cancer } are shown along the top of the table. The probabilities in the blue area are the joint probabilities for observing pairs of outcomes — e.g., \(X = \mbox{Smoker}\) and \(Y = \mbox{No Cancer}\). The probability that \(X=x\) and \(Y=y\) can be written in a few ways: \(\Pr(X=x \, \mbox{and} \, Y=y)\), \(\Pr(X=x, Y=y)\), or \(\Pr(x,y)\). They’re all equivalent. For brevity, we’ll tend to use the last version.
As an example, the probability that a randomly selected person is a nonsmoker who never develops lung cancer is \[\Pr(\mbox{Nonsmoker}, \mbox{No Cancer}) = .7657\] Another way to think about this is to imagine that we go through the above process (i.e., randomly select someone from the computer database and look at their values of \(X\) and \(Y\)) over and over and over, say a million times. About 76.57% of the time we randomly select someone, they’ll be a nonsmoker with no cancer.
Similarly, the probability that a randomly selected person is a smoker who eventually develops lung cancer is \[\Pr(\mbox{Smoker}, \mbox{Cancer}) = .055\] Again, if we were to go through this exercise (i.e., randomly select someone from the computer database and look at their values of \(X\) and \(Y\)) a million times, about 5.5% of the time we’ll pick someone who is a smoker with cancer.
Notice that blue area provides joint probabilities for every possible pair of values for \(X\) and \(Y\). Just as when we considered a single random variable, the joint probabilities over the pairs of outcomes must sum to one. Check for yourself that \[.7657 + .0075 + .1718 +.055 = 1\]
Marginal Probabilities: They’re in the Margins
The probabilities outside the blue area are marginal probabilities. The right side probabilities under the label \(\Pr(x)\) are the marginal probabilities for \(X\): \[\Pr(X=\mbox{Nonsmoker})=.7732\] and \[\Pr(X=\mbox{Smoker}) = .2268\] This is simply the probability distribution for RV \(X\) when we’re not considering its joint distribution with another RV. For example, the probability that a randomly selected person is a smoker is .2268. And, just like before, \(X\)’s marginal probabilities must sum to one.
The marginal probabilities for \(Y\) are shown along the bottom, next to the label \(\Pr(y)\). These are the same probabilities that were shown at the beginning of this chapter. Again, \(Y\)’s marginal probabilities must sum to one: \(\Pr(\mbox{No Cancer}) + \Pr(\mbox{Cancer}) = .9375+.0625 =1\).
Finally, the marginal and joint probabilities are related in a straightforward manner:
A row’s joint probabilities must sum to the row marginal probability.
A column’s joint probabilities must sum to the column marginal probability.
Example 1: The marginal probability \(\Pr(\mbox{No Cancer})\) is equal to the sum of the joint probabilities in its column.
| Y | ||||
| No Cancer | Cancer | Pr(x) | ||
| X | Nonsmoker | 0.7657 | 0.0075 | 0.7732 |
| Smoker | 0.1718 | 0.055 | 0.2268 | |
| Pr(y) | 0.9375 | 0.0625 | ||
\[\begin{align} \Pr(\mbox{No Cancer}) & = .9375\\ & = \Pr(\mbox{Nonsmoker, No Cancer}) + \Pr(\mbox{Smoker, No Cancer})\\ & = .7657 + .1718 \end{align}\]
Example 2: The marginal probability \(\Pr(\mbox{Smoker})\) is equal to the sum of the joint probabilities in its row.
| Y | ||||
| No Cancer | Cancer | Pr(x) | ||
| X | Nonsmoker | 0.7657 | 0.0075 | 0.7732 |
| Smoker | 0.1718 | 0.055 | 0.2268 | |
| Pr(y) | 0.9375 | 0.0625 | ||
\[\begin{align} \Pr(\mbox{Smoker}) & = .2268\\ & = \Pr(\mbox{Smoker, No Cancer}) + \Pr(\mbox{Smoker, Cancer})\\ & = .1718 + .055 \end{align}\]
Practice Session: Joint and Marginal Probabilities
In this practice session, you are shown the joint distribution for two discrete random variables, \(X\) and \(Y\). The table below shows the joint probabilities \(\Pr(x,y)\) in blue. Marginal probabilities \(\Pr(x)\) are shown on the right. Marginal probabilities \(\Pr(y)\) are shown along the bottom. Somewhere in the joint or marginal probabilities is a missing value, labeled NA. Calculate the missing probability, enter it in the box in the left panel, and click Submit. Try another problem by hitting Next. Repeat the exercise four or five times, or until you feel comfortable calculating joint and marginal probabilities in such a table.
Remember:
1. Joint probabilities must sum to one.
2. Each set of marginal probabilities must sum to one.
3. A row \(\Pr(x)\) value is the sum of the joint probabilities in that row.
4. A column \(\Pr(y)\) value is the sum of the joint probabilities in that column.
Practice Session: Joint and Marginal Probabilities \(\times\) 3
In this practice session, like the prior practice session, you are shown the joint distribution for two discrete random variables, \(X\) and \(Y\). The table below shows the joint probabilities \(\Pr(x,y)\) in blue. Marginal probabilities \(\Pr(x)\) are shown on the right. Marginal probabilities \(\Pr(y)\) are shown along the bottom.
Here, however, there are three missing probabilities labeled NA: one joint probability, one marginal probability for \(X\), and one marginal probability for \(Y\). Calculate the missing probabilities, enter them in the appropriate boxes in the left panel, and click Submit. Try another problem by hitting Next. Repeat the exercise four or five times, or until you feel comfortable calculating joint and marginal probabilities in such a table.
Remember:
1. Joint probabilities must sum to one.
2. Each set of marginal probabilities must sum to one.
3. A row \(\Pr(x)\) value is the sum of the joint probabilities in that row.
4. A column \(\Pr(y)\) value is the sum of the joint probabilities in that column.
19.2 Conditional Probability
As we saw in the last section, the joint probability distribution for two RVs \(X\) and \(Y\) tells us the probability of randomly drawing a specific pair of outcomes for \(X\) and \(Y\). For example, what is the probability that a randomly selected person is a smoker with no cancer? The joint probability \(\Pr(\mbox{Smoker, No Cancer})=.1718\).
| Y | ||||
| No Cancer | Cancer | Pr(x) | ||
| X | Nonsmoker | 0.7657 | 0.0075 | 0.7732 |
| Smoker | 0.1718 | 0.055 | 0.2268 | |
| Pr(y) | 0.9375 | 0.0625 | ||
Now, suppose you work for an insurance company and you already have (or know) the joint distribution above for US residents. Further, suppose you receive new insurance applications from two people. One writes down that they’re a smoker. The other states that they are a nonsmoker. Assume both are telling the truth. How does knowing that a person is a smoker change the probability that they will eventually develop lung cancer? We’ll write the probability of developing lung cancer, given that a person smokes as \(\Pr(\mbox{Cancer} | \mbox{Smokes})\). Similarly, the probability that a person develops cancer, given that they do not smoke is \(\Pr(\mbox{Cancer} | \mbox{Nonsmoker})\). The pipe or bar \(|\) tells us that everything after it is “given” or assumed known.
If we have two random variables \(X\) and \(Y\), the probability that \(Y=y\), given that \(X=x\) is defined as \[\Pr(Y=y | X=x) = \frac{\Pr(Y=y, X=x)}{\Pr(X=x)}\] Similarly, \[\Pr(X=x| Y=y) = \frac{\Pr(X=x Y=y)}{\Pr(Y=y)}\] And, as before, we will use the abbreviated version in writing these: \(\Pr(y|x) = \frac{\Pr(x,y)}{\Pr(x)}\).
Continuing with our running example, given that someone is a nonsmoker, the probability of eventually developing lung cancer is \[\Pr(\mbox{Cancer}|\mbox{Nonsmoker})=\frac{\Pr(\mbox{Nonsmoker, Cancer})}{\Pr(\mbox{Nonsmoker})}=\frac{.0075}{.7732}=.00969\] Given that someone is a smoker, the probability of eventually developing lung cancer is \[\Pr(\mbox{Cancer}|\mbox{Smoker})=\frac{\Pr(\mbox{Smoker, Cancer})}{\Pr(\mbox{Smoker})}=\frac{.055}{.2268}=.2425\] Let’s compare these numbers. If we know someone is a nonsmoker, they have a less than a 1% chance of developing lung cancer. On the other hand, if someone is a smoker, they have over a 24% chance of developing lung cancer. Although the joint probabilities in each case look relatively small — .0075 and .055 — once we condition on whether a person is a smoker versus nonsmoker, the probabilities change dramatically.
Interactive Example: Conditional Probability
In this example, you are shown the joint distribution for two discrete random variables, \(X\) and \(Y\). RV \(X\) takes on numeric values (left column of the table). RV \(Y\) takes on alphabetical values (top row of the table). Joint probabilities \(\Pr(x,y)\) are shown as blue cells in the table. Marginal probabilities \(\Pr(x)\) are displayed in the rightmost column. Marginal probabilities \(\Pr(y)\) are shown at the bottom of the table.
The purpose of the example is to demonstrate how to calculate conditional probabilities. An outcome of \(X\) or \(Y\) has been selected. The example assumes that value is “given” – i.e., we are conditioning on that outcome. The conditioning outcomes row or column is highlighted in a slightly darker shade of blue. The marginal probablity for the conditioning variable is highlighted in red.
Conditional probability calculations are displayed below the table. You can generate a new distribution and conditioning variable by clicking on Show Another. Repeat the exercise four or five times, or until you feel comfortable calculating conditional probabilities.
Practice Session: Conditional Probability
This practice session is similar to the interactive example above, except that now you are asked to calculate a conditional probability.
You are provided the joint distribution for two discrete random variables, \(X\) and \(Y\). RV \(X\) takes on numeric values (left column of the table). RV \(Y\) takes on alphabetical values (top row of the table). Joint probabilities \(\Pr(x,y)\) are shown as blue cells in the table. Marginal probabilities \(\Pr(x)\) are displayed in the rightmost column. Marginal probabilities \(\Pr(y)\) are shown at the bottom of the table.
Calculate the joint probability shown below the table and enter it in the box in the left panel. When you click Submit, you’ll be shown whether your answer is correct or not. Click Next to try another problem. Repeat the exercise four or five times, or until you feel comfortable calculating conditional probabilities.
19.3 Independence
Practice Session: Independence
In this practice session, you are shown the joint distribution for two discrete random variables, \(X\) and \(Y\). Determine whether \(X\) and \(Y\) are independent. Make your selection by choosing the radio button in the left panel and then click Submit. Refresh the distribution by hitting Next. Repeat the exercise four or five times, or until you feel comfortable checking for independence.
Note: You can also treat this as an interactive example. Simply hit Next and then Submit for each new example. If the default answer is incorrect, the correct answer and a short explanation will be displayed at the bottom.
19.4 The Binomial Distribution (Optional)
The Binomial distribution is an extension of the Bernoulli. In fact, it is built on multiple Bernoulli trials. Suppose we have \(k\) Bernoulli “trials” or experiments. In each case, we observe either a success \(X=1\) or a failure \(X=0\). Further, suppose each Bernoulli trial has the same success probability \(\Pr(X=1)=\pi\). Finally, and here’s the kicker, suppose we don’t observe the individual Bernoulli trials. Instead, someone tells us only the number of trials that were sucesses (\(X=1\)). In the Binomial distribution, our random variable of interest, \(Y\), is the number of successes out of \(k\) Bernoulli trials, when each trial has success probability \(\pi\).
Let’s suppose now that \(Y\) is distributed Binomial(\(k\),\(\pi\)). What are the possible outcomes? As specified, there are \(k\) Bernoulli trials. (It’s important to note that \(k\) is a parameter defining the Binomial distribution. It is not an outcome.) On the lower end, all of the trials could be failures (\(X=0\)), so the minimum value of \(Y\) is 0. On the upper end, all of the trials could be successes (X=1), so the maximum value is \(Y=k\). Therefore, given \(k\) trials, the possible outcomes are \(Y \in \{ 0, 1, 2, \ldots , k \}\).
Given \(Y \sim \mbox{Binomial}(k,\pi)\) with possible outcomes \(Y \in \{ 0, 1, 2, \ldots , k \}\), what is the Binomial pmf – i.e., the probability \(\Pr(y | k, \pi)\) for each possible outcome? That’s a bit more complicated. The complicating issue is that we don’t observe the individual Bernoulli trials; we only observe the total number of successes. Imagine that there are four trials. We re told that two of trials were successes. We don’t know which of the four were successes. In the Binomial probability \(\Pr(2 | k=4, \pi)\), we have to take into account that two successes could have occurred in multiple ways in the four trials. The table below shows the ways in which we could observe two success in four trials: \[\begin{array}{lcccc} & \mbox{Trial 1} & \mbox{Trial 2} & \mbox{Trial 3} & \mbox{Trial 4} \\ \hline \mbox{Possibility 1:} & 1 & 1 & 0 & 0 \\ \mbox{Possibility 2:} & 1 & 0 & 1 & 0 \\ \mbox{Possibility 3:} & 1 & 0 & 0 & 1 \\ \mbox{Possibility 4:} & 0 & 1 & 1 & 0 \\ \mbox{Possibility 5:} & 0 & 1 & 0 & 1 \\ \mbox{Possibility 6:} & 0 & 0 & 1 & 1 \\ \hline \end{array}\]
The Binomial probability \(\Pr(2 | k=4, \pi)\) of \(y=2\) successes in \(k=4\) trials is the probability that one of those six possibilities occurs. In the end, we’ll need to add the probabilities for each of the possibilities in the table. Using the Bernoulli success probability \(\pi\) for the trials, we can write the probability of observing each of the row outcomes as \[\begin{array}{lccccc} & \mbox{Trial 1} & \mbox{Trial 2} & \mbox{Trial 3} & \mbox{Trial 4} & \mbox{Row Probability} \\ \hline \mbox{Possibility 1:} & \pi & \pi & 1-\pi & 1-\pi & \pi^2 (1-\pi)^2 \\ \mbox{Possibility 2:} & \pi & 1-\pi & \pi & 1-\pi & \pi^2 (1-\pi)^2\\ \mbox{Possibility 3:} & \pi & 1-\pi & 1-\pi & \pi & \pi^2 (1-\pi)^2 \\ \mbox{Possibility 4:} & 1-\pi & \pi & \pi & 1-\pi & \pi^2 (1-\pi)^2 \\ \mbox{Possibility 5:} & 1-\pi & \pi & 1-\pi & \pi & \pi^2 (1-\pi)^2 \\ \mbox{Possibility 6:} & 1-\pi & 1-\pi & \pi & \pi & \pi^2 (1-\pi)^2 \\ \hline \end{array}\]
Notice that each of the possibilities (rows) has the same probability \(\pi^2 (1-\pi)^2\). Each \(\pi\) is for a Bernoulli success in that row and each \((1-\pi)\) is for a Bernoulli failure. Now, we don’t know which of the rows really occurred. So the Binomial probability \(\Pr(2 | k=4, \pi)\) is actually the probability of possibility 1 + the probability of possibility 2 + \(\cdots\) + probability of possibility 6. Since each possibility has the same probability, the resulting Binomial probability is \(\Pr(2 | k=4, \pi) = 6 \times \pi^2 (1-\pi)^2\).
More generally, if we have \(k\) Bernoulli trials, each with success probability \(\pi\), then the pmf for the number of success \(Y\) is \[\Pr(y | k, \pi) = \left(\begin{array}{c} k \\ y \end{array} \right) \, \pi^y \, (1-\pi)^{k-y}\] where \[\left(\begin{array}{c} k \\ y \end{array}\right) = \frac{k!}{y! (k-y)!}\] is the “Binomial coefficient” and represents the number of ways we can obtain \(y\) successes in \(k\) trials.
Interactive Example: Binomial Pr(y successes | k trials, \(\pi\))
The following interactive example provides intuition for the Binomial probability \(\Pr(y | k, \pi)\) – i.e., the probability of \(y\) successes in \(k\) Bernoulli trials, where each Bernoulli trial has a success probability of \(\pi\). The example allows you to change the parameters of the distribution \(k\) and \(\pi\). You can also change the value of \(y\), the number of successes. Read through the example for the default values. Then change one or all of the parameters. Read through the example again. Depending on which parameters changed, the table, equations, and numerical results may change as well. Work through enough examples until you feel like you understand the underlying math behind Binomial probabilities.